#05 - Estimation du nombre pi#
Énoncé#
Écrire un programme qui calcule une estimation de la valeur du nombre pi avec une approche probabiliste.
Calcul de PI par la méthode de Monte-Carlo
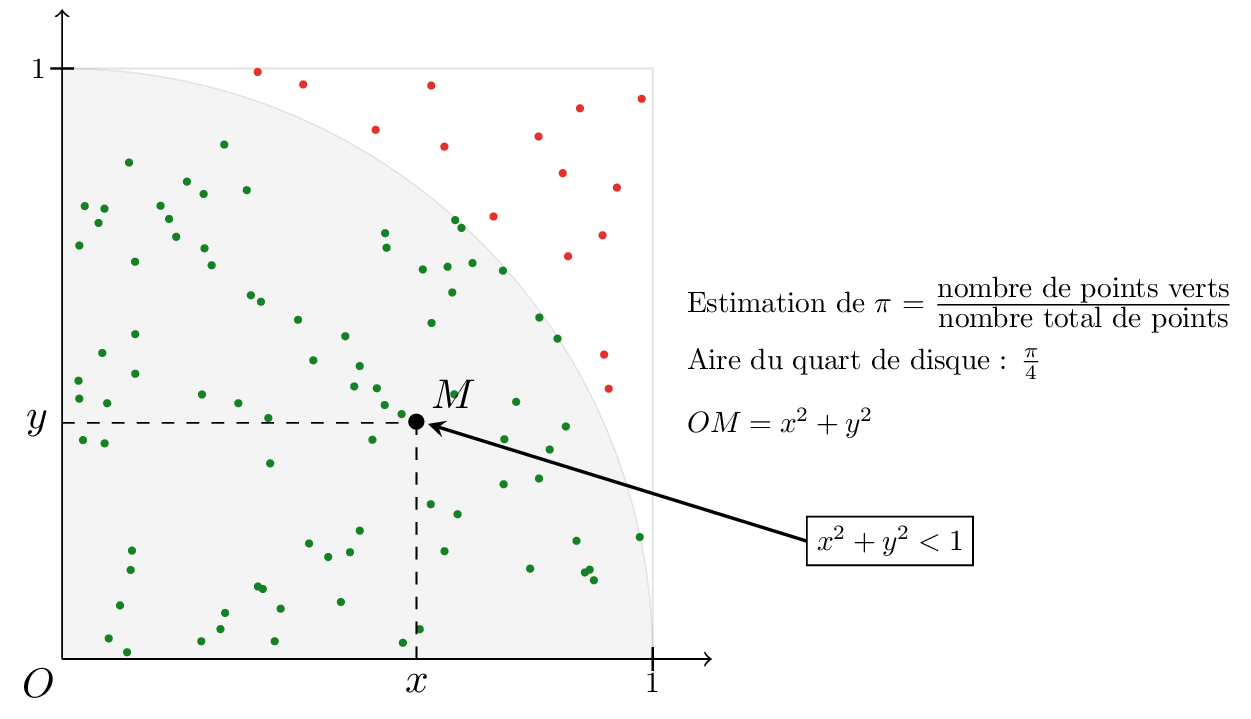
Le calcul de π par la méthode de Monte-Carlo consiste à tirer au hasard des nombres x et y dans l'intervalle [0 ; 1].
Si x² + y² < 1 le point M (x, y) appartient à un quart de disque de rayon 1. La probabilité pour qu'il en soit ainsi est le rapport des aires du quart de disque de rayon 1 et du carré de côté 1 et soit π / 4.
Dans cette appliquette n est le nombre total de points générés par une suite pseudo-aléatoire, p est le nombre de points à l'intérieur du quart de disque et 4 p / n donne par conséquent une valeur approchée de π.
--> Soure: https://jpq.pagesperso-orange.fr/proba/montecarlo/index.htm
Solution#
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define RAYON 1
#define MIN 0
#define MAX 123456
#define MINTIRS 10
#define MAXTIRS 1000000000
int TirerUnPoint(void)
{
float xTire, yTire, dist;
int estdanslecercle=1;
// On tire un point dans le quart du carré [0, 1]×[0, 1]
xTire=1.0*(rand()%(MAX-0+1)-MIN)/MAX;
yTire=1.0*(rand()%(MAX-0+1)-MIN)/MAX;
dist=xTire*xTire + yTire*yTire;
if (dist>RAYON*RAYON)
{
estdanslecercle=0;
}
return estdanslecercle;
}
void CalculerPi(int nombreDeTirs)
{
int i, ncercle=0;
float surface, pi;
for (i=0; i<nombreDeTirs; i++)
{
ncercle+=TirerUnPoint();
}
// p/n
surface=(1.0*ncercle)/nombreDeTirs;
// calcul de pi
pi=4*surface;
printf("Ntirs: %d\t\t\tpi: %f\n", nombreDeTirs, pi);
}
int main()
{
int i;
srand(time(NULL));
for (int i=MINTIRS; i<=MAXTIRS; i*=10)
{
CalculerPi(i/2);
CalculerPi(i);
}
return 0;
}