Régression linéaire simple avec Tensorflow

Dans cette première section de la formation Tensorflow, je vous présente les tenseurs élément fondamental et enfin vous verrez comment apprendre une régression linéaire.

Importation

L'API Keras est très utilisée, donc on l'importe également. Pour rappel Keras a été intégré dans Tensorflow.

import tensorflow as tf
from tensorflow import keras

Les tenseurs

Un tenseur est un tableau multidimensionnel qui contient des données de même type. Les tenseurs sont semblables aux tableaux Numpy np.array. Un tenseur peut être une valeur scalaire semblable à une variable classique Python.

Exemple d'un tenseur scalaire :

scalar = tf.constant(2)
print(scalar)

[Output]

tf.Tensor(2, shape=(), dtype=int32)

Exemples de tenseurs :

tf_vector = tf.constant([1, 0, -5, 4])
print(tf_vector)

tf_matrix = tf.constant([[1, 0, -5, 4], [1, 0, -5, 3]])
print(tf_matrix)

[Output]

tf.Tensor([ 1  0 -5  4], shape=(4,), dtype=int32)

tf.Tensor(
[[ 1  0 -5  4]
 [ 1  0 -5  3]], shape=(2, 4), dtype=int32)

La méthode .numpy() permet de convertir les tenseurs TensorFlow en tableaux Numpy. Par exemple, pour convertir tf_vector en tableau Numpy :

numpy_vector = tf_vector.numpy()
print(numpy_vector)

[Output]

[ 1  0 -5  4]

Pour en savoir plus sur les tenseurs, consultez la docs officielle Introduction aux tenseurs.

Apprentissage itératif

Lapprentissage des modèles avec Tensorflow se fait de manière itérative. Si la régression linéaire possède une solution directe, la solution peut-être approchée de manière itérative.

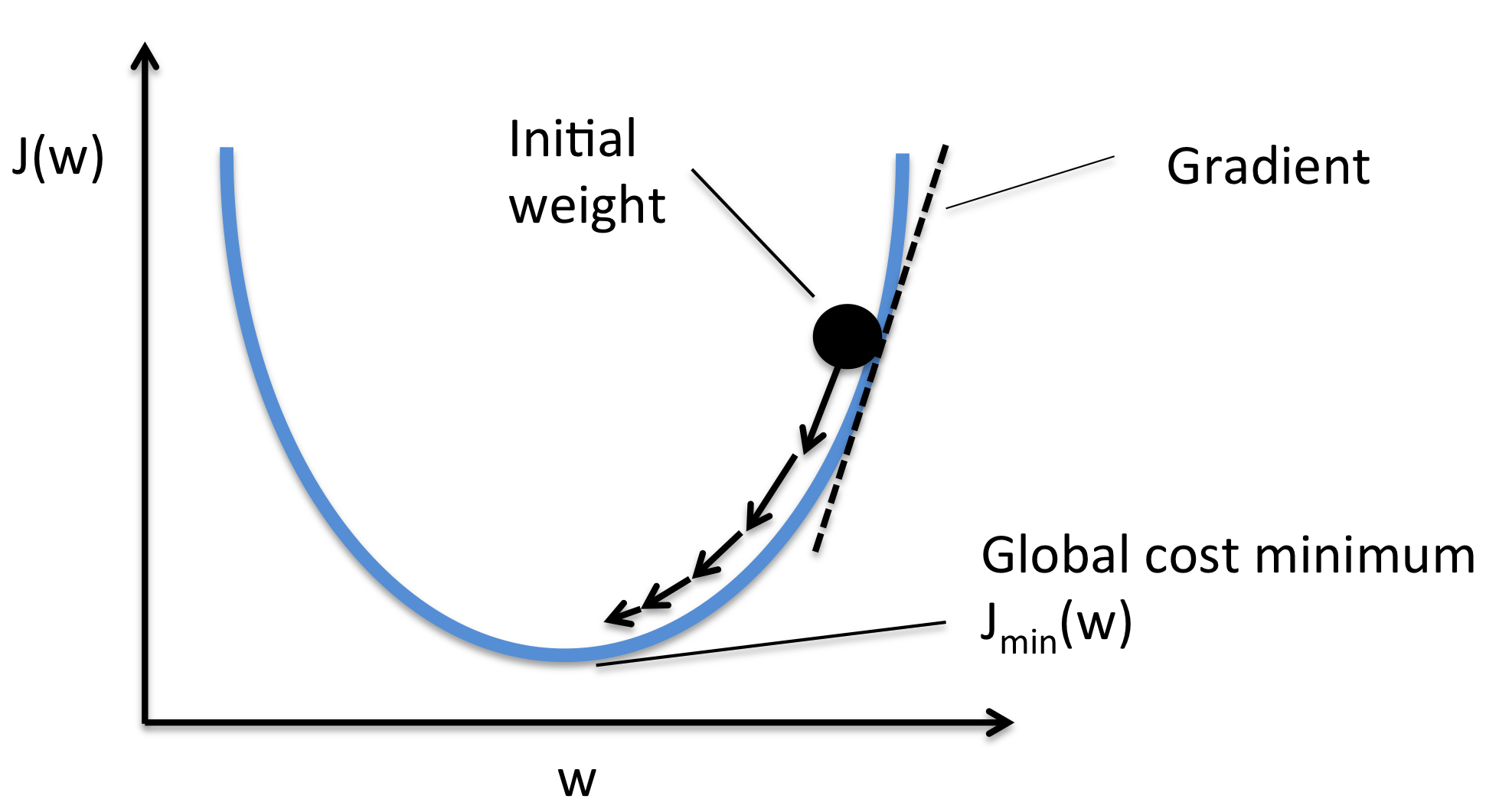
La solution directe devient impossible lorsque la taille des données est trop grande pour tenir en memoire. On doit donc passer à un mode d'apprentissage itératif avec des mini-lots.

Régression linéaire

Nous allons résoudre notre premier problème de machine learning avec Tensorflow. Il s'agit d'un exercice simple, nous allons réaliser une régression linéaire simple avec Tensorflow.

Pour rappel, une régression linéaire est de la forme suivante:
\(y = aX + b + \epsilon\)
où a et b sont les paramètres du modèle et \(\epsilon\) le résidu.

Jeu de données

Nous allons simuler un jeu de données fictif avec \(a=2\) et \(b=1\) en plus d'un résidu qui suit la normale centrée réduite.

import numpy as np

np.random.seed = 42

n_samples = 200
X = np.linspace(-10, 10, n_samples)
y = X*2 + 1 + np.random.normal(0, 1, n_samples)

print(X.shape, y.shape)

[Output]

(200,) (200,)

Nuage de points

Nous allons représenter les données sur un graphique pour illustrer la relation linéaire. Pour cela nous utilisons le package Matplotlib.

plt.scatter(X, y)
plt.show()

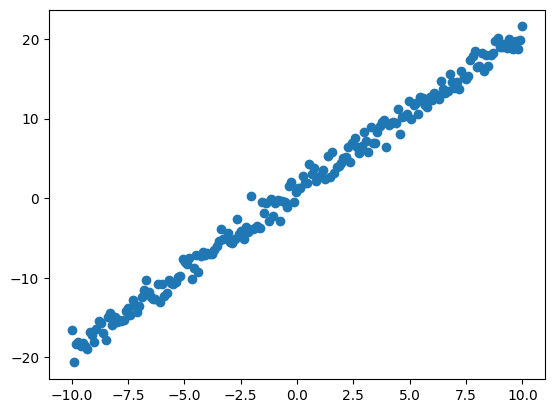
Premier modèle avec Tensorflow

Nous allons à présent créer le modèle en utilisant Keras.

model = keras.Sequential(keras.layers.Dense(1, input_shape=(1,)))
model.summary()

[Output]

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 1)                 2         

=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________

Paramétrage de l'apprentissage

Le paramétrage consiste à définir la fonction de perte et la méthode d'optimisation à utiliser pendant l'apprentissage.

model.compile(loss="mse", optimizer="sgd")

Entraînement

Nous allons entraîner le modèle sur 10 époques avec des mini-lots de données de 20.

model.fit(X, y, batch_size=20, epochs=10)

Analyse du résultat

a, b = tuple(np.array(model.layers[0].weights))
print("a = ", a)
print("b = ", b)

[Output]

a =  [2.023662567138672]
b =  [0.8865243792533875]

Les valeurs estimées pour \(a\) et \(b\) sont respectivement \(2.02\) et \(0.89\). Ces valeurs sont assez proches de celles utilisées pendant la simulation du jeu de données, l'approximation est plutôt bonne.

C'est important de comprendre que cette notion d'approximation parce que c'est en cela que consiste la régression linéaire et l'apprentissage automatique en général.

plt.scatter(X, y, label="Dataset")
plt.plot([X[0], X[-1]], [X[0] * a + b, X[-1] * a + b], c="red", label="Regression Curve")
plt.legend(loc="best")
plt.show()

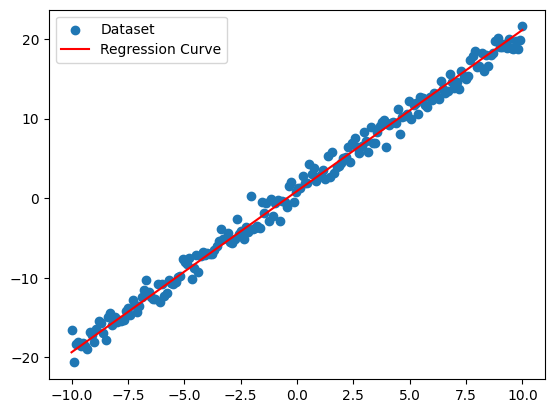
On peut voir sur le graphique ci-dessus que le modèle rend assez bien compte des données.

Comparaison True Y vs Predicated Y

y_pred = model(X).numpy()

plt.scatter(y, y_pred)
plt.title("True Y vs Predicted Y")
plt.xlabel("True Y")
plt.ylabel("Predicted Y")
plt.show()

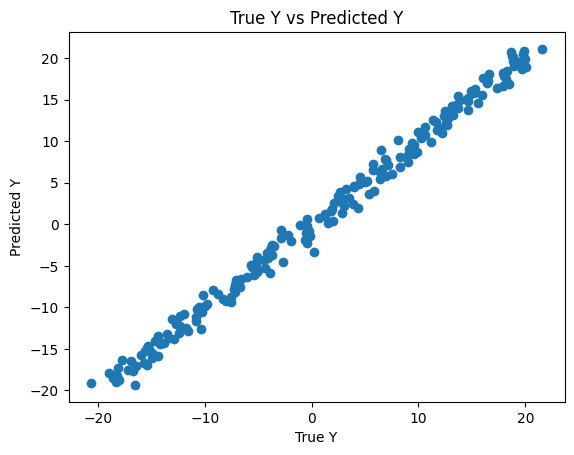
Dans un monde parfait, on aurait eu une droite mais puisqu'il s'agit d'approximation les valeurs prédites sont très proches des vraies valeurs.

Code complet

import tensorflow as tf
from tensorflow import keras

model = keras.Sequential(keras.layers.Dense(1, input_shape=(1,)))
model.summary()

model.compile(loss="mse", optimizer="sgd")

model.fit(X, y, batch_size=20, epochs=10)

a, b = tuple(np.array(model.layers[0].weights))
print("a = ", a)
print("b = ", b)

plt.scatter(X, y, label="Dataset")
plt.plot([X[0], X[-1]], [X[0] * a + b, X[-1] * a + b], c="red", label="Regression Curve")
plt.legend(loc="best")
plt.show()

y_pred = model(X).numpy()

plt.scatter(y, y_pred)
plt.title("True Y vs Predicted Y")
plt.xlabel("True Y")
plt.ylabel("Predicted Y")
plt.show()

---

Bravo ! Vous venez de créer votre premier modèle avec Tensorflow. Dans la prochaine section, nous verrons comment créer des réseaux de neurones avec Tensorflow.